1. 에라토스테네스의 체란?
제목 그대로 소수를 판별하는 알고리즘으로서 소수들을 대량으로 빠르게 구할 수 있는 방법이다. O(N^1/2)의 시간복잡도를 갖는다.
원리
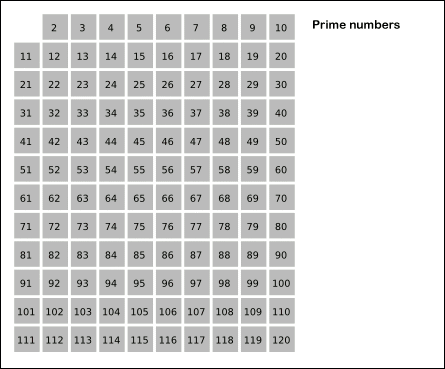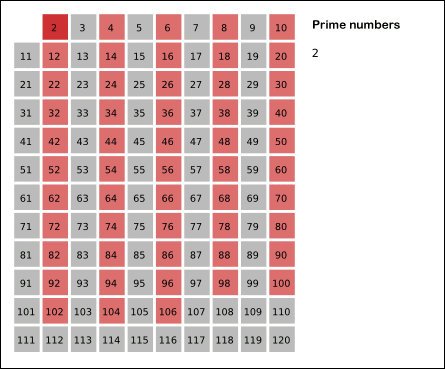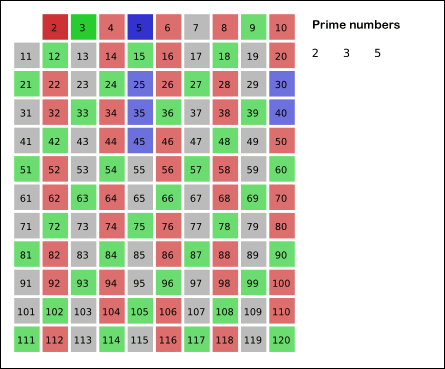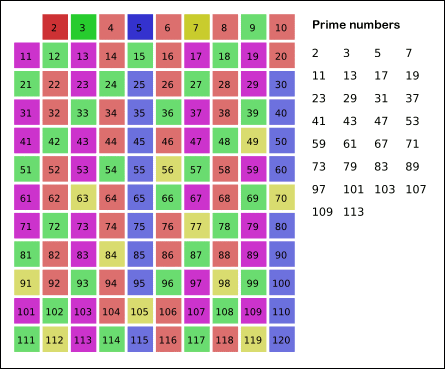
소수란 1과 자기자신만을 약수로 갖는 수를 의미한다. 즉, 1을 제외한 어떤 수의 배수가 되는 수들은 모두 소수가 아니다. 에라토스테네스의 체는 이러한 소수의 특성을 이용한다.
임의의 수 n 까지의 소수를 구하고자 할 때, 2부터 n의 제곱근까지 돌며 모든 배수들을 소수에서 제거시키는 방식으로 동작한다.
2. 구현 (c++)
using namespace std;
int n;
int prime[1001];
void primeNum(){
// prime 배열 초기화
for (int i = 2; i <= n; i++){
prime[i] = i;
}
for (int i = 2; i <= sqrt(n); i++)
{
if (!prime[i]) //이미 소수가 아니면
continue;
for (int j = i * i; j <= n; j += i) //어떤 수의 배수는 소수가 아님
prime[j] = 0;
}
// 소수 출력
for (int i = 2; i <= n; i++)
{
if (prime[i])
cout << prime[i] << " ";
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n;
primeNum();
}
'알고리즘 공부 및 문제 풀이 > 알고리즘(ALGORITHM)' 카테고리의 다른 글
| [pro] 프로그래머스 level3 12907 거스름돈 (Java) - dp (0) | 2023.01.27 |
|---|---|
| [알고리즘] 최단 경로 알고리즘(3) - 플로이드 워셜(Floyd-Warshall) 알고리즘 (0) | 2022.10.25 |
| [알고리즘] 최단 경로 알고리즘(2) - 다익스트라(Dijkstra) 알고리즘 (0) | 2022.10.25 |
| [알고리즘] 최단 경로 알고리즘(1) - 벨만 포드(Bellman Ford) 알고리즘 (0) | 2022.10.25 |
| [알고리즘] 세그먼트 트리(Segment Tree) (0) | 2022.06.20 |


