1. 벨만-포드 알고리즘이란?
그래프 상에서 최단 경로를 찾는 알고리즘 중 하나이다. 또 다른 최단 경로 알고리즘인 다익스트라에 비교해서 간선의 가중치가 음수여도 가능하지만 다익스트라에 비해 수행 시간이 더 오래 걸린다는 단점이 있다.
다익스트라 알고리즘이 그리디 알고리즘인 반면 벨만-포드 알고리즘은 다이나믹 프로그래밍을 기본 개념으로 한다. 이전에 계산해 저장된 최단 경로를 이용해서 새로운 최단 경로를 갱신하는 방식이다. 그리디하지 않게 동작하기 때문에, 모든 경우의 수를 탐색하는 동작 방식을 취한다.

시작 노드 s에서 v로 가는 최단 경로는 s에서 u로의 최단 경로 + u와 v 사이에 가중치를 더한 값으로 계산된다.
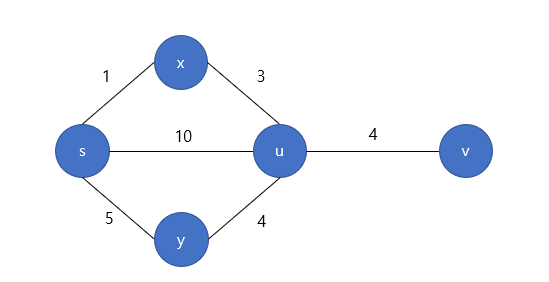
정점의 개수가 N개라면 N-1 개의 간선을 선택해 값을 갱신한다. (N-1이 아닌 N번의 검사를 통해 갱신되는 값이 있다면 음의 사이클이 존재하는 것이다.) 간선의 선택 개수를 N-1까지 증가해가며 최소 가중치합을 비교해서 최소값을 계속 유지시키게 된다.
위 과정을 통해 시작 정점 s에서 도착 정점 v로 가는 최단경로는 dist[x] = 1, dist[u] = dist[x] + 3, dist[v] = dist[u] + 4,
1 + 3 + 4 = 8로 갱신 될 것이다.
2. 진행 과정 & 구현(c++)
1. 초기의 최소 비용을 저장하는 int dist[] 배열을 최소값을 비교해서 저장해주기위해 INF로 초기화한다.
2. 시작 정점을 0으로 해주고, 모든 간선들을 탐색하면서 시작 정점이 INF가 아니라면(한번이라도 계산된 적이 있는 정점이라면) 해당 간선이 잇는 정점의 거리를 비교해서 갱신 해준다.
3. N-1번 검사를 반복한다.
void bellman_ford(){
dist[0] = 0;
for(int i=1; i<=n-1; i++){
for(int j=0; j<edge.size(); j++){
int cost = edge[j].first;
int s = edge[j].second.first;
int e = edge[j].second.second;
if(dist[s]==INF) continue;
if(dist[e] > dist[s] + cost)
dist[e] = dist[s] + cost;
}
}
for(int j=0; j<edge.size(); j++){
int cost = edge[j].first;
int s = edge[j].second.first;
int e = edge[j].second.second;
if(dist[s]==INF) continue;
if(dist[e] > dist[s] + cost){
cout << "음의 사이클이 존재함." << "\n"; //음의 사이클 존재
return;
}
}
cout << "음의 사이클이 존재하지 않음.";
}
'알고리즘 공부 및 문제 풀이 > 알고리즘(ALGORITHM)' 카테고리의 다른 글
| [알고리즘] 최단 경로 알고리즘(3) - 플로이드 워셜(Floyd-Warshall) 알고리즘 (0) | 2022.10.25 |
|---|---|
| [알고리즘] 최단 경로 알고리즘(2) - 다익스트라(Dijkstra) 알고리즘 (0) | 2022.10.25 |
| [알고리즘] 세그먼트 트리(Segment Tree) (0) | 2022.06.20 |
| [알고리즘] 백트래킹(Backtracking) 알고리즘 (0) | 2021.08.02 |
| [알고리즘] 동적프로그래밍(Dynamic programming) (0) | 2021.07.21 |



